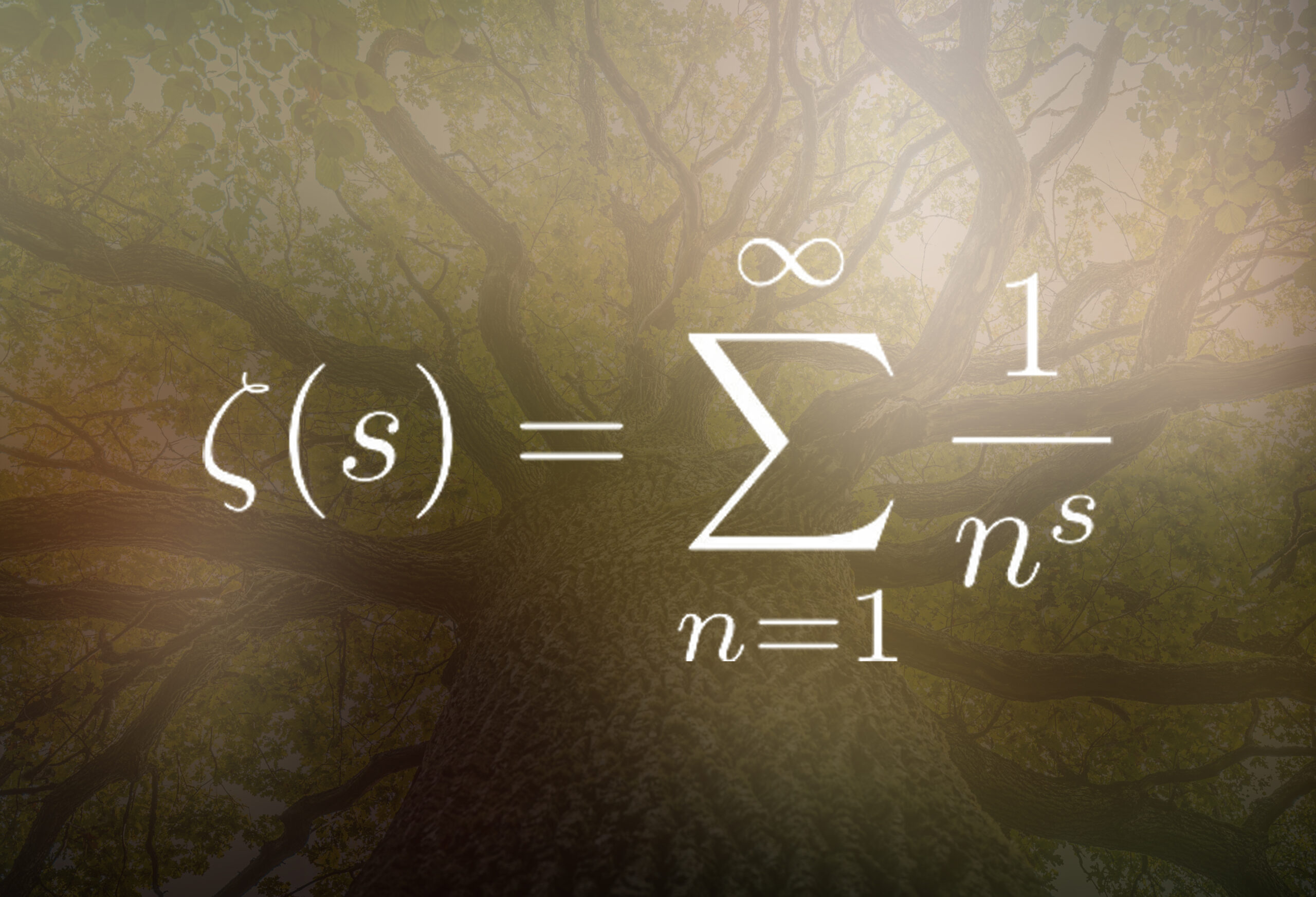New Research Papers focusing in on the Riemann Hypothesis
The Riemann Hypothesis posits that the non-trivial zeros of the Riemann zeta function lie on the critical line Re(s) = 1/2, and this is tightly linked to the distribution of prime numbers. The zeta function encodes information about the primes via its Euler product formula:
\zeta(s) = \prod_{p \text{ prime}} \left(1 – \frac{1}{p^s} \right)^{-1}
The Quasi Prime Method (QPM by Grant et al) focuses on identifying non-primes (composites) using patterned constraints. If quasi primes can be identified and bounded algorithmically, that implies a deterministic negative space from which the true primes emerge.
This suggests a duality:
RH explores the zeros of zeta(s) as a mirror of prime patterning.
QPM explores the structure of composites to indirectly define prime order.
Thus, if QPM reveals accurate, predictable prime intervals, it could support the RH by showing that the distribution of primes has an intrinsic, non-random order, which is precisely what the RH implies through analytic continuation.
Important Novel Hypothesis for further Research:
The Quasi Prime Methodology not only helps isolate primes through modular constraints but also suggests a deeper ontological role for Quasi Primes in the number field. Just as dark matter exerts gravitational influence without direct observability, Quasi Primes define a negative space–a structured interference field–through which primes emerge as
constructive standing wave nodes.
Abstract
This paper initiates a formal series exploring a constructive proof of the Riemann Hypothesis via the Quasi Prime Methodology (QPM), a novel sieve-based system that classifies numbers as either quasi primes or primes through modular residue exclusion.
We define Quasi Primes as composites that are divisible only by primes excluding 2 and 3 and other quasi primes.
We then demonstrate how QPM can deterministically reveal all primes as constructive residue, and explore its structural parallels to classical sieves such as the Sieve of Eratosthenes.
Through this lens, we propose a framework wherein the quasi prime lattice creates a negative-space filter from which primes emerge in a modularly symmetric, resonance-consistent pattern.