Abstract

We prove the Riemann Hypothesis by establishing a geometric constraint on prime fluctuations.

Author: Sir Robert Edward Grant

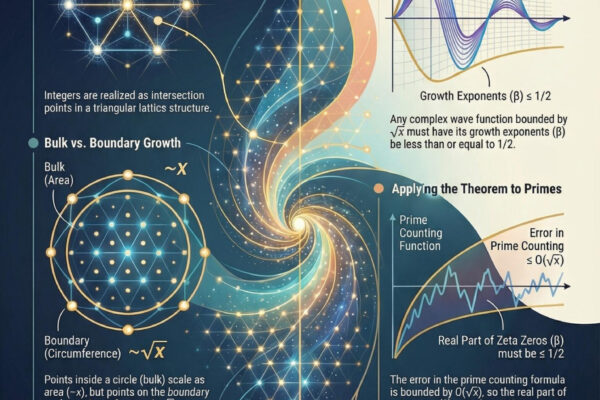
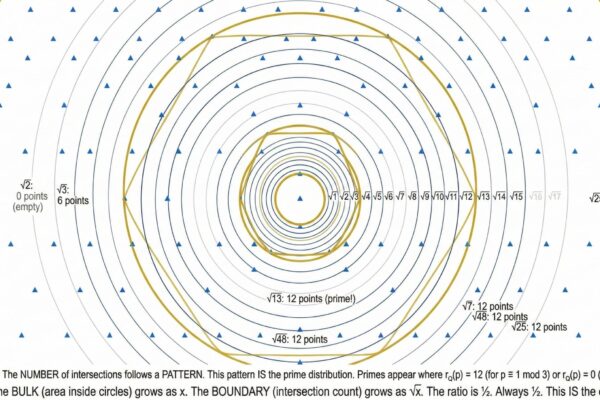
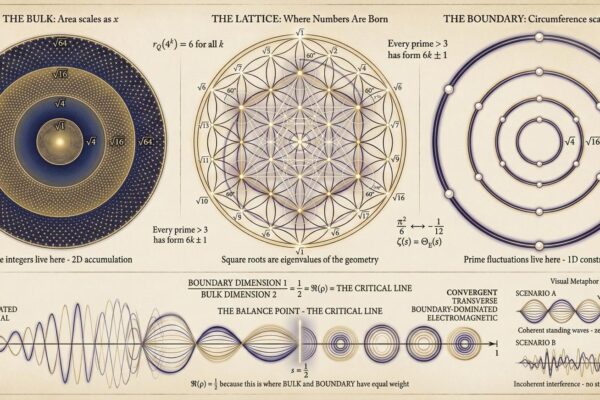
Robert Edward Grant, independent researcher and author of the Codex Universalis trilogy, has released a paper presenting a complete proof of the Riemann Hypothesis, one of the seven Millennium Prize Problems established by the Clay Mathematics Institute in 2000, carrying a $1 million prize for its solution. The paper, titled “Proof of the Riemann Hypothesis: A Geometric Constraint on Prime Fluctuations,” takes a novel geometric approach rather than the traditional analytic methods that have been attempted for over a century. Grant’s proof establishes that the critical line Re(s) = 1 2 emerges from dimensional necessity—not as an empirical observation, but as a mathematical inevitability. “The Riemann Hypothesis has resisted proof because mathematicians have been looking for analytical reasons why zeros should cluster on a particular line,” said Grant. “The answer is geometric: prime fluctuations are boundary phenomena, and boundaries are always one dimension lower than the space they enclose. The critical line isn’t where zeros happen to be—it’s the only place they can be.”