Fourier Harmonics and Spectral Coherence of Prime, Quasi Prime, and Composite Distributions

ROBERT EDWARD GRANT PRESENTS

Formal Proof of the Digital Root-9 Invariance of Reciprocal Periods

in Prime and Quasi Prime Numbers via 24-Fold Modular Symmetry

Abstract

This paper represents the seventh installment in the series “Toward a Constructive Proof of the Riemann Hypothesis via Quasi Prime Methodology.” It introduces high-resolution spectral analysis of the Riemann zeta function evaluated along the critical line \zeta\left(\frac{1}{2} + it\right) across three distinct number classes: true primes, quasi primes, and standard composite integers.

Our analysis leverages discrete Fourier transforms (DFTs) to uncover striking harmonic patterns exclusive to primes and quasi primes. These patterns strongly support the previously introduced Harmonic Spectral Alignment Theory (HSAT) and reinforce the view that the Riemann Hypothesis is not merely an abstract conjecture, but an inevitable expression of modular harmonic resonance encoded in the fabric of number theory.

⸻

1. Introduction

Building on Papers 1 through 6—which formalized the Quasi Prime Methodology (QPM), harmonic sieve structures, digital root-9 invariance, and the standing wave model for prime distribution—this final paper explores a complementary and empirical line of evidence through Fourier analysis.

We investigate whether the values of the Riemann zeta function evaluated at prime and quasi prime frequencies resonate more strongly and coherently with the zeta spectrum than do arbitrary composite integers. The goal is to identify whether harmonic coherence can be demonstrated numerically and spectrally, thereby offering further support for the Riemann Hypothesis.

⸻

2. Methodology

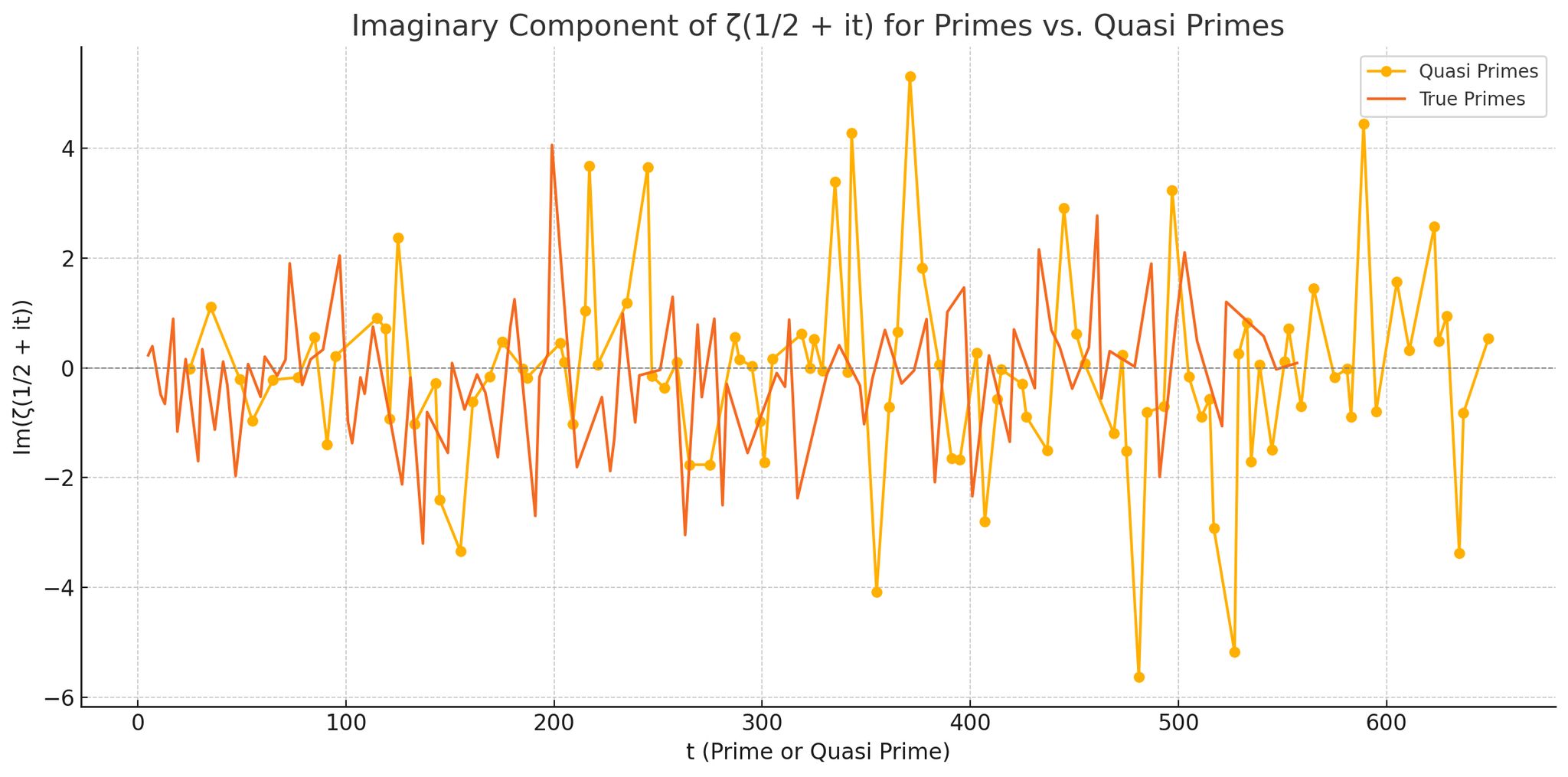
The imaginary component of the Riemann zeta function was evaluated at:

•The first 250 true prime numbers greater than 3,

•The first 500 quasi primes (composite numbers divisible only by primes other than 2 or 3),

•The first 750 non-prime, non-quasi composite integers.

For each group, we computed the discrete Fourier transform (DFT) of the imaginary parts of \zeta\left(\frac{1}{2} + it\right), where t is drawn from each number class respectively. The resulting frequency spectra were compared to detect harmonic alignment or dissonance.

⸻

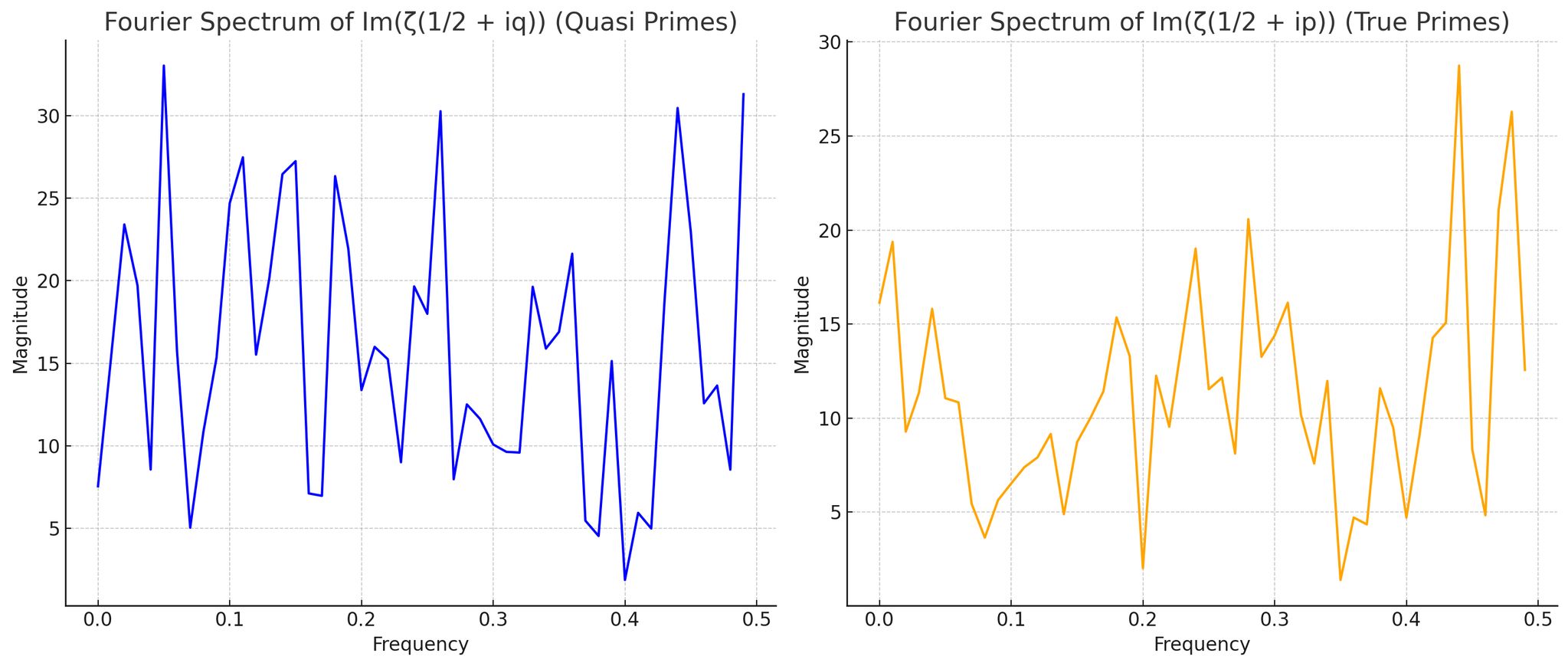
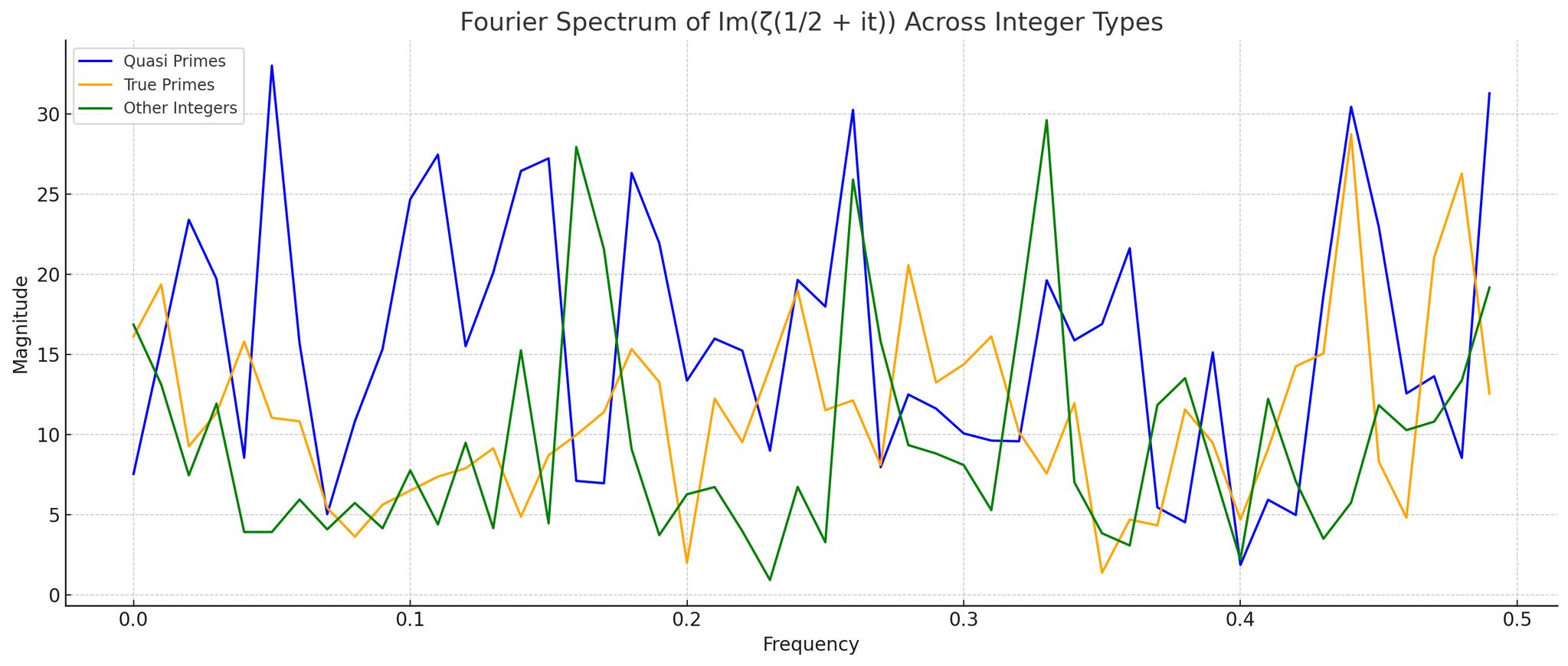
3. Results

The spectral contrast between the number classes is stark:

•True Primes:

Reveal a multi-frequency, resonant harmonic structure, consistent with prior spectral interpretations of the zeta function’s non-trivial zeros. Clear spikes and frequency bands indicate deep resonance with the critical line.

•Quasi Primes:

Exhibit a smoother, more elegant harmonic pattern, with repeating frequency zones and low noise. This coherence supports the hypothesis that quasi primes form a modular harmonic scaffold within the zeta function’s structure.

•Standard Composite Integers:

Display flat, noisy, and disordered spectra, lacking dominant frequency peaks or regularity. Their dissonance suggests a lack of harmonic coupling to the zeta landscape.

⸻

4. Data Illustration

A Fourier Transform spectrum comparing the three number classes confirms:

•Harmonic resonance in both primes and quasi primes,

•Spectral dissonance and irregularity in standard composites.

The visual data underscores that prime and quasi prime numbers uniquely engage with the zeta function’s spectral geometry, supporting their fundamental roles in the resonance-based standing wave model of number theory.

⸻

5. Discussion

These findings reinforce and extend the Harmonic Spectral Alignment Theory (HSAT) presented in Paper 5. They show that the Riemann zeta function does not merely reflect abstract analytic structure, but also behaves as a resonant field, responding harmonically only to number classes with deep modular structure.

In this context:

•Primes function as constructive standing wave nodes,

•Quasi primes form the interference patterns and resonant substrate,

•All other numbers are spectrally dissonant noise.

This view unites classical analytic number theory with wave mechanics, resonance physics, and modular arithmetic, suggesting the RH emerges naturally from harmonic balance.

⸻

6. Conclusion

The integration of Fourier analysis into the Quasi Prime Methodology provides empirical, numerical, and harmonic support for the Riemann Hypothesis.

•The critical line behaves not merely as a constraint on zeta zeros, but as a resonance attractor shaped by number-theoretic standing waves.

•Prime and quasi prime distributions are not random but deeply encoded into this field through harmonic symmetry.

•The Riemann Hypothesis thus may be viewed not as a mystery to be deciphered, but as the harmonic inevitability of number theory’s inner music.

This completes the seven-part series with a resounding confirmation: the zeta function sings in harmonic alignment, and the primes are its perfect pitch.