Authors: Robert E. Grant, Talal Ghannam, Naomi Mathew
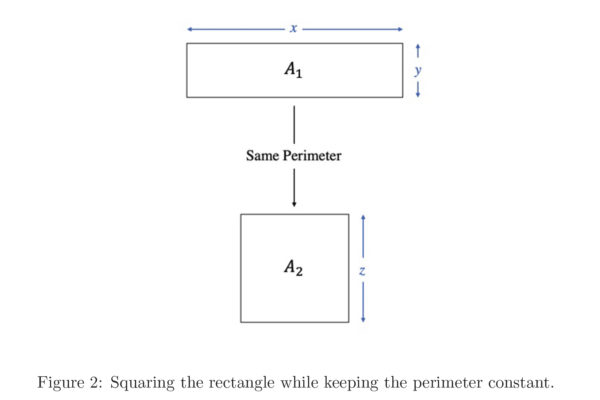
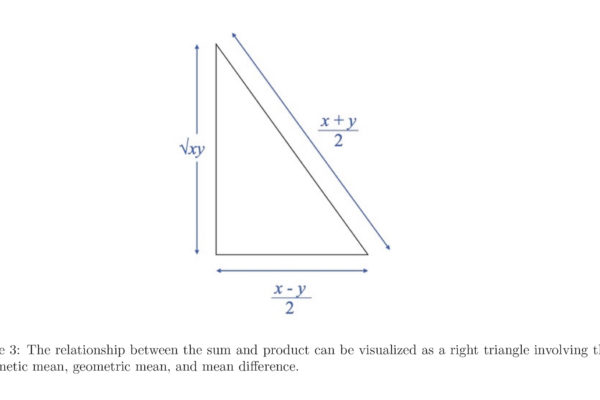
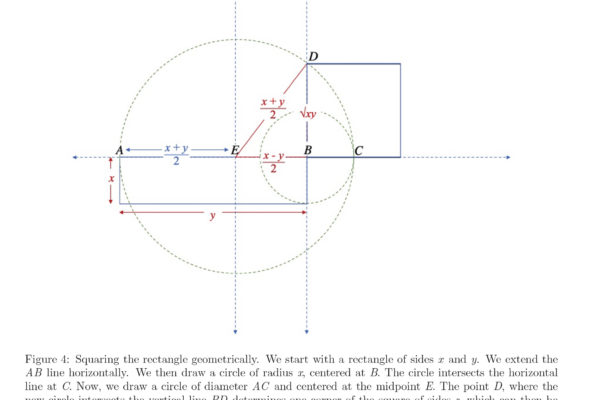
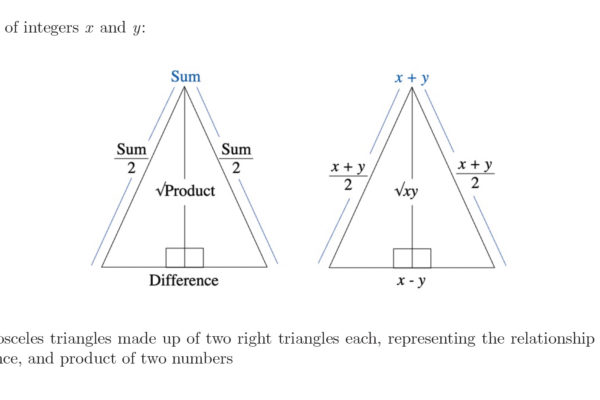
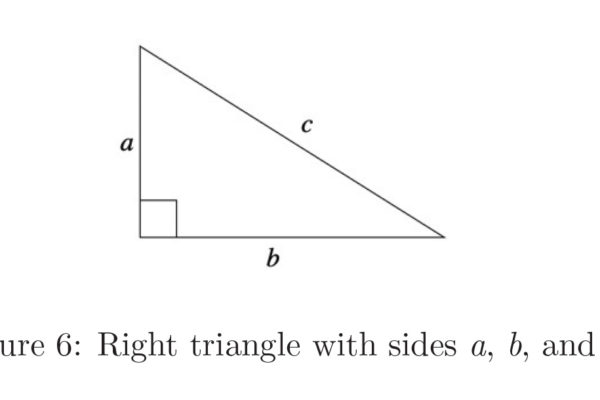
In this paper, we re-derive Fermat’s factorization identity through a geometrical approach. We exploit its Pythagorean triangle configuration to investigate the relationship between the sum of two numbers and their product. This visual perspective of numbers enhances our understanding of their nature, equipping us with the tools to tackle unsolved problems in number theory with a completely new approach.
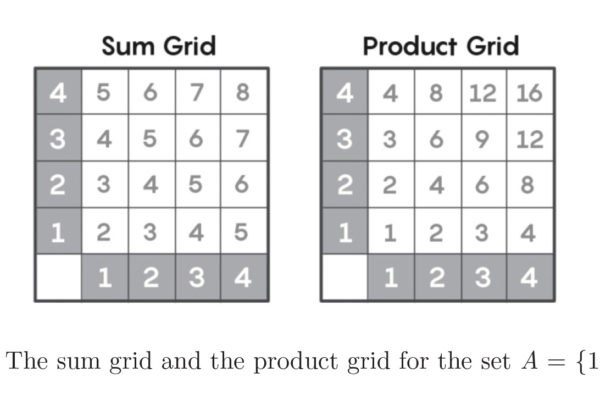
Although addition and multiplication are widely considered to be relatively simple operations in mathematics, little is known about the relationship between the sum of two numbers and their product. This open problem in number theory has been difficult to solve. One breakthrough was the Erdos Szemeredi Theorem, which was proven in 1983. Rather than directly defining a relationship between the sum and product, Paul Erdos and Endre Szemeredi approached this problem by comparing the sum grid for a set of integers to its product grid.