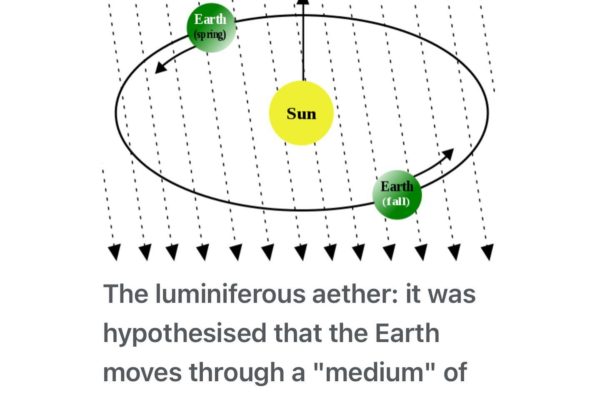
Is it time to revisit the concept of the ‘Luminiferous Aether’ that was abandoned, (perhaps prematurely), in the early 20th Century?
The Aether is a concept (supported by such cosmological/physics luminaries as Nikola Tesla, Walter Russell, Paul Dirac, Michelson-Morley and Herbert Ives) that needed mathematics (and experimentation) to back it up.
With our (Grant, Ghannam et al) recent publication titled: ‘A Novel Geometric Model of Natural Spirals Based on Right Triangle ‘Polygonal’ Modular Formations’ (Cornell University’s ArXiv.org) we may now have pathways for both….
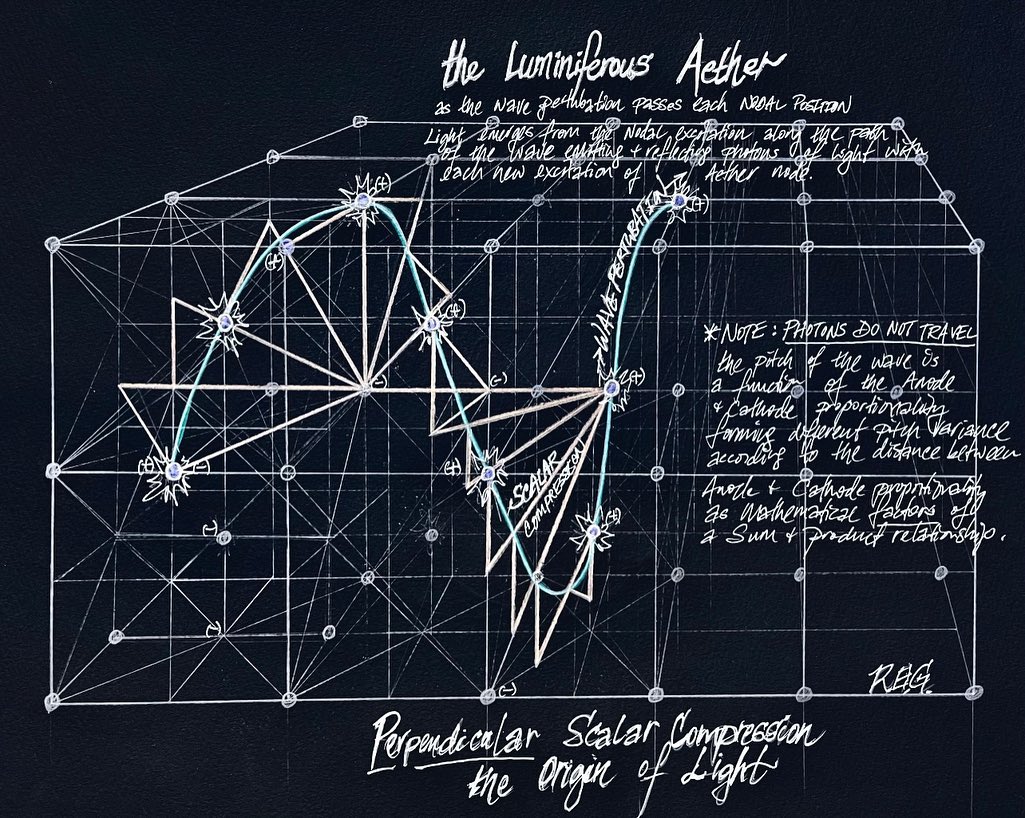
The illustration below is a potential mathematical approach to demonstrating the concept of the Luminiferous Aether based upon the relationship between the Product and the Sum of two ‘parental’ (prime) numbers. This relationship reveals that EVERY Triangle (including Scalene and Isosceles) possess two ‘parental’ (numerical value) numbers that ultimately reveal their Logarithmic Base through the following equation: Arithmetic Mean (= x+y*1/2) / Geometric Mean (= x*y^1/2).
In this approach, as the Wave perturbation passes each nodal position light (photons) emerge from the nodal ‘excitation’ caused by the wave perturbation. The Aether field is excited by sine-cosine (transverse and longitudinal) spirals with pitch specific to their commencing fractality specifically by the Hypotenuse/Height (Log Base Value) of two coordinates (x;y)3: Anode and Cathodes defined by the wave perturbation in the form of Right Triangles. Right triangles are unique in that all polygons and all Polyhedra are formed without void space between Right Triangles.
NOTE: This thesis proposes that Photons DO NOT actually travel; rather, they are merely light reflections of the Aether field’s nodal excitations. (Nodal points in the path of the wave are excited by (wave) perturbations causing both the reflection and absorption (of light photons).
We may indeed now have a general thesis from which to work from based upon the Sum Product Conjecture paper we (Talal Ghannam PhD, Naomi Matthews and myself) also wrote and published recently. You can read the paper HERE.