NEW DISCOVERY
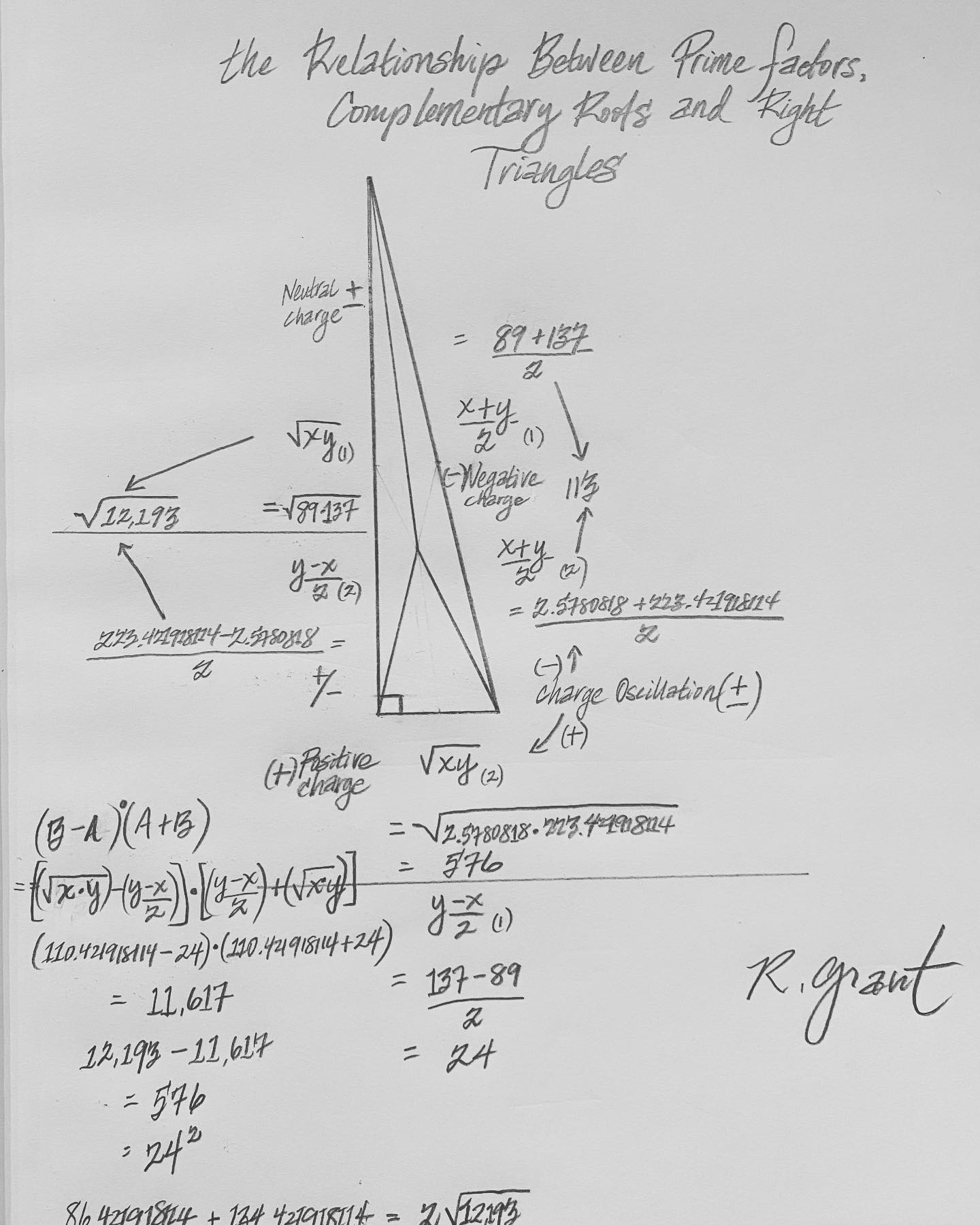
(Boxing Day, 2020): THE COMPLEMENTARY ROOT. ALL Numbers can be expressed as a Pythagorean Right Triangle. These triangles reveal their symmetries and factors. Consider the Pythagorean Theorem: A^2 + B^2 = C^2. When B is the square root of a Quasi Prime Number (Product of two primes >3), C-A = Prime1; and C+A = Prime2.
ADDITIONAL NEW DISCOVERY: C-B = Complementary Root1; C+B = Complementary Root2. These Complementary Root values are MIRROR SYMMETRY complements to Prime1 and Prime2, imagine a mirrored Right Triangle that switches the role of Side A and Side B. They also have other very unique characteristics: 1.). Both values are infinite irrational values. 2.) The decimal extensions are “complementary” infinitely: the decimal tails always SUM to ONE. 3. When multiplied together, though irrational, they multiply together to produce a perfectly WHOLE number value which informs the Side A^2 value of the Right Triangle that will be a PERFECT SQUARE Value (meaning it’s Square Root will be a Whole Number).
This means that every number has two COMPLEMENTARY Irrational values that multiply to CREATE that number (and not only the irrational Square Root as previously believed). For example: Quasi Prime Number 30,607 will yield a Triangle with the following Side Lengths: A= 57; B= 30,607^.5 = 174.9485638694985…; and C= 184. The Prime factors therefore are derived as: C-A = 127; and C+A = 241. NOW, let’s calculate the Complementary Root values: C-B = 9.051436130501488….; C+B = 358.9485638694985….First, notice how the decimal extension is a mirror match to the Square Root of 30,607; Second, notice that the two decimal extensions sum precisely to ONE. Now, let’s multiply the Two Complementary Root values together: Result = 3,249, and notice that this is indeed a Perfect Square value as its Square Root = 57 (the precise value of Side A!). Notice also that the (Sum of the two Complementary Root values)/2 = Side C (184).
This is TRUE for every Pythagorean Triangle and reveals yet ANOTHER newly discovered mathematical relationship for numbers: The (Irrational) Complementary Roots of Numbers.